Расчетно-экспериментальная оценка надежности выполняется на различных этапах проектирования и изготовления вагонов. Исходными данными для этого являются: характеристики режима нагрузки (эксплуатационные силы, кинематические воздействия); структура проектируемого вагона с указанием типа и количества составляющих элементов и их взаимосвязи в смысле надежности; статические характеристики несущей способности элементов для заданных режимов нагрузки; сведения о функциональных зависимостях между свойствами и характеристиками составляющих элементов и вагона в целом (аналитические или эмпирические формулы для оценки прочности вагона, зависимость между напряжениями, нагрузками и геометрическими характеристиками вагона).
Эти данные в теории надежности называются априорной экспериментальной информацией.
Существуют два основных вида расчетов надежности вагона:
а) расчет надежности всего вагона по известным показателям структуры конструкции вагона;
б) расчет надежности детали или конструкции вагона в целом на основе использования статистических закономерностей изменения внешней нагрузки и несущей способности с учетом физической природы отказов.
В ряде случаев оба вида расчетов выполняются совместно. Расчет структурной (схемной) надежности вагона в целом можно выполнять, если известна надежность отдельных его элементов и характер их взаимодействия.
По условиям надежности различают следующие структурные схемы соединения элементов вагона: последовательное соединение, при котором отказ любого элемента вызывает отказ вагона в целом; параллельное соединение, при котором отказ вагона в целом происходит только при отказе всех элементов, соединенных между собой параллельно, например, параллельное соединение нескольких ремней или валов привода вагонного генератора системы электроснабжения пассажирских вагонов; параллельно-последовательное соединение, в котором имеется система с после¬довательным соединением нескольких блоков, связанных между собою параллельно.
Расчет надежности при внезапных отказах вагона выполняется исходя из того, что изменение нагрузки различных элементов вагона часто представляет собой стационарный нормальный случайный процесс, т.е. с постоянными во времени параметрами (математическое ожидание, дисперсия), а распределение мгновенных значений нагрузок на вагон подчиняется нормальному закону распределения случайных величин. Задача расчета надежности вагона состоит в определении вероятности выброса случайного процесса в течение заданного отрезка времени. Например, можно вести расчет на вероятность превышения напряжениями предела текучести материалов, из которых построен вагон.
Расчет надежности вагона при внезапных отказах можно вести также в квазистатической постановке, если режим нагрузки представляет собой систему дискретных воздействий, например, удары в автосцепку или случайный процесс колебаний вагона схематизируется как совокупность случайных величин. В этом случае статическая характеристика нагруженности вагона представляется как распределение случайных величин сил со своими параметрами.
Сущность этого метода расчета надежности состоит в следующем. Сопоставляются статические распределения внешней силовой нагрузки и несущей способности вагона, под ко¬торой понимается предельная нагрузка, которую может выдержать вагон без разрушения.
Расчет надежности вагона с использованием метода статических испытаний (метод Монте-Карло), который в последнее время применяется достаточно широко, дает возможность изучать влияние на надежность различных статических факторов и функциональной связи между ними, т.е. дает возможность обеспечить системный подход к расчету, что особенно важно при расчетах надежности вагонов на перспективу.
Для использования этого метода расчета надежности необходимо иметь достаточно полную априорную экспериментальную информацию, а именно: составить математическую модель, связывающую искомую характеристику с влияющими на нее факторами; получить статистические характеристики распределения каждого фактора.
В основе статических испытаний лежит возможность получения на электронной вычислительной технике (компьютере) случайных чисел с различными законами распределения соответственно каждому фактору влияния. Процесс испытаний состоит в многократных расчетах по заданной аналитической зависимости (математической модели), при этом для каждого расчета принимаются свои случайно выбранные значения факторов, тем самым воспроизводятся условия проявления факторов в эксплуатации. В результате многократных расчетов получают много значений искомой характеристики надежности, например долговечности, и по ним строят ее распределение, которое позволяет ответить на основной вопрос о вероятности безотказной работы вагона за определенный промежуток времени. Важным принципом этого метода является порядок операций по выбору факторов.
Этот метод применим также и для решения промежуточных задач, например, для определения закона распределения нагрузки или несущей способности.
Расчет надежности при усталостных отказах от случайных нагрузок в большинстве случаев выполняется на основе гипотезы о линейном суммировании усталостных повреждений при циклических нагрузках. В методике такого расчета широко применяются два основных направления. В первом направлении, разработанном в институте машиноведения СВ. Серенсеном и В.П. Когаевым, расчетные нагрузки представляются в виде блоков сил или напряжений, отражающих закономерность их изменения в течение определенного времени, например за год, а распределение времени безотказной работы предположительно подчиняется заранее принятому закону распределения случайных величин, обычно применяется логарифмически нормальный закон. В основном расчет сводится к определению средней долговечности детали или узла вагона с учетом среднего значения предела выносливости детали при базовом числе циклов нагружения, амплитуд напряжений, относительного числа циклов нагрузки, числа циклов расчетных нагрузок за год.
Второе направление основано на разработанной В.В. Болотиным методике расчета долговечности при усталостных разрушениях и использовании метода Монте-Карло. Главная особенность этого направления состоит в введении расчетной нагрузки в форме плотности распределения амплитуд напряжений характерного для рассматриваемого стационарного случайного процесса нагрузки. При этом предположений о законе распределения времени безотказной работы заранее не делается, а он определяется с применением метода Монте-Карло, для чего задаются характеристиками распределения значений времени безотказной работы вагона.
В рассмотренных расчетах надежности вагона предполагается, что заданные вероятностные характеристики нагруженности и несущей способности остаются неизменными в течение всего времени эксплуатации.
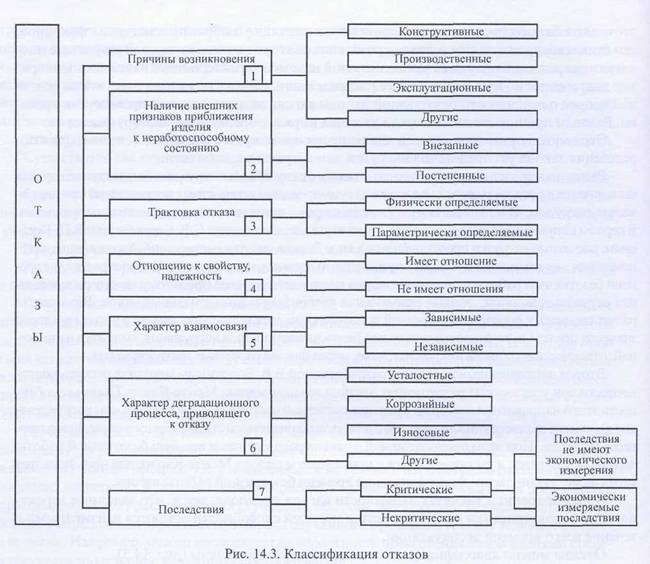
Отказы можно классифицировать по различным признакам (рис. 14.3).